物理學(xué)家麥克斯韋預(yù)言光是電磁波，這在光學(xué)歷史上是一次革命，從此宇宙中最神秘的光被統(tǒng)治在麥克斯韋方程組之下。

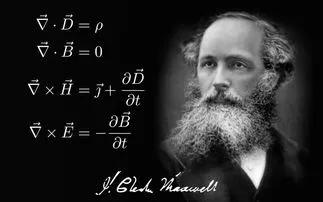
1.電磁波

電磁波：由相同且互相垂直的電場(chǎng)與磁場(chǎng)在空間中衍生發(fā)射的震蕩粒子波，是以波動(dòng)的形式傳播的電磁場(chǎng)，具有波粒二象性。電磁波是由同相振蕩且互相垂直的電場(chǎng)與磁場(chǎng)在空間中以波的形式移動(dòng)，其傳播方向垂直于電場(chǎng)與磁場(chǎng)構(gòu)成的平面。電磁波在真空中速率固定，速度為光速。

電磁波伴隨的電場(chǎng)方向，磁場(chǎng)方向，傳播方向三者互相垂直，因此電磁波是橫波。當(dāng)其能階躍遷過輻射臨界點(diǎn)，便以光的形式向外輻射，此階段波體為光子，太陽(yáng)光是電磁波的一種可見的輻射形態(tài)，電磁波不依靠介質(zhì)傳播，在真空中的傳播速度等同于光速。電磁輻射由低頻率到高頻率，主要分為：無線電波、微波、紅外線、可見光、紫外線、X射線和伽馬射線。人眼可接收到的電磁波，稱為可見光（波長(zhǎng)380~780nm）。電磁輻射量與溫度有關(guān)，通常高于絕對(duì)零度的物質(zhì)或粒子都有電磁輻射，溫度越高輻射量越大，但大多不能被肉眼觀察到。

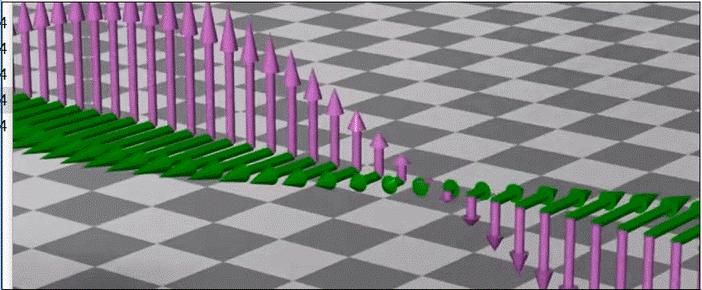
頻率是電磁波的重要特性。按照頻率的順序把這些電磁波排列起來，就是電磁波譜。如果把每個(gè)波段的頻率由低至高依次排列的話，它們是無線電波、微波、紅外線、可見光、紫外線、X射線及γ射線。

2.頻率

頻率（frequency）：?jiǎn)挝粫r(shí)間完成振動(dòng)的次數(shù)，是描述振動(dòng)物體往復(fù)運(yùn)動(dòng)頻繁程度的量，常用符號(hào)f或v表示。每個(gè)物體都有由它本身性質(zhì)決定的與振幅無關(guān)的頻率，叫做固有頻率。它們的特征參量是波長(zhǎng)λ、頻率f和光子能量E。三者的關(guān)系是f=c/λ，E=hf=hc/λ和E=1.24/λ，式中，E和λ的單位分別是eV（電子伏）和μm，h為普朗克常數(shù)（6.6260755X10J·S）；c為光速，其真空中的近似值等于3X10m/s，在工程實(shí)踐中，根據(jù)不同的需要和習(xí)慣，采用不同的頻譜參量計(jì)量單位。

3.光子能量

光子能量( photon energy)：光子即光量子（light quantum），傳遞電磁相互作用的規(guī)范粒子，記為γ。其靜止質(zhì)量為零，不帶電荷，其能量為普朗克常量和電磁輻射頻率的乘積，即E=hv，在真空中以光速c運(yùn)行，單位為焦（J）·秒（s）。

4.光的干涉

光的干涉（Interference of light）：物理學(xué)中，干涉（interference）是兩列或兩列以上的波在空間中重疊時(shí)發(fā)生疊加從而形成新的波形的現(xiàn)象。兩列波在同一介質(zhì)中傳播發(fā)生重疊時(shí)，重疊范圍內(nèi)介質(zhì)質(zhì)點(diǎn)同時(shí)受到兩個(gè)波的作用。若波的振幅不大，此時(shí)重疊范圍內(nèi)介質(zhì)質(zhì)點(diǎn)的振動(dòng)位移等于各別波動(dòng)所造成位移的矢量和，這稱為波的疊加原理。若兩波的波峰（或波谷）同時(shí)抵達(dá)同一地點(diǎn)，稱兩波在該點(diǎn)同相，干涉波會(huì)產(chǎn)生最大的振幅，稱為相長(zhǎng)干涉；若兩波之一的波峰與另一波的波谷同時(shí)抵達(dá)同一地點(diǎn)，稱兩波在該點(diǎn)反相，干涉波會(huì)產(chǎn)生最小的振幅，稱為相消干涉。　　

5.什么條件下會(huì)發(fā)生光的干涉光的干涉條件？

準(zhǔn)確的說，應(yīng)該是兩列相干光可以發(fā)生干涉，任何一個(gè)光束都不可能是絕對(duì)的單色光，也可說絕對(duì)不可能只有單一頻率。所以，任何一個(gè)光源只要滿足時(shí)間相干性，都可以發(fā)生干涉，比如一束光的波長(zhǎng)是600nm-601nm，另外一束光是600.5nm-601.5nm，他們的頻率成分當(dāng)中（頻率就是光速除以波長(zhǎng)）有相同的部分，如果滿足時(shí)間相干性，也就是相干頻率大于他們直接的頻率差就可以干涉！另外就是滿足空間相干性，任何一個(gè)光源，可以是光源上不同兩個(gè)地方發(fā)出的光線，只要這兩個(gè)發(fā)光的部分的長(zhǎng)度小于空間相干長(zhǎng)度，就也可以發(fā)生干涉！關(guān)于相位差恒定，也是不必要條件，只要大致穩(wěn)定就行，舉例說明：比如，雙縫干涉，當(dāng)屏幕不動(dòng)的時(shí)候，光程差是恒定的，也可以說是相位差是恒定的，當(dāng)光屏向后或者向前移動(dòng)的時(shí)候，相位差肯定會(huì)變，條紋間距也會(huì)變，變寬或者變窄，但是干涉圖樣始終存在，說明相位差變化了，只能使得干涉圖樣發(fā)生波動(dòng)，但是不穩(wěn)定的相位差一樣可以發(fā)生干涉！震動(dòng)方向一致也是非必要條件，只要震動(dòng)方向不垂直，兩個(gè)互成角度的震動(dòng)，可以向力的分解那樣，把震動(dòng)分為一致方向和垂直方向，一致方向的分量依然可以和另外一個(gè)震動(dòng)發(fā)生干涉，只不過干涉圖樣的明暗對(duì)比度會(huì)下降，而只要當(dāng)完全垂直的時(shí)候，對(duì)比度才下降為零，才可以認(rèn)為是不干涉。

綜上所述：頻率相同，位相差恒定，振動(dòng)方向一致的相干光源是發(fā)生“穩(wěn)定”干涉的條件，而非發(fā)生干涉的條件。

6.非偏振光

“非偏振”光的光子取向隨機(jī)。來自光源的一個(gè)單光子的電場(chǎng)被定向在給定的方向上，下一個(gè)光子的電場(chǎng)將被定向在不同的方向。通常，光子全部以不同方向的電場(chǎng)發(fā)射。最常見的非偏振光源是太陽(yáng)光。然而，電場(chǎng)的取向在反射，折射以及散射時(shí)會(huì)改變。到達(dá)觀察者的間接太陽(yáng)光具有優(yōu)選的電場(chǎng)取向，這通常被稱為“部分偏振”光。它用來表示具有未明確定義的優(yōu)選取向的電場(chǎng)。

7.偏振光

偏振光（ polarized light ）：振動(dòng)方向?qū)τ趥鞑シ较虻牟粚?duì)稱性叫做偏振，它是橫波區(qū)別于其他縱波的一個(gè)最明顯的標(biāo)志，只有橫波才有偏振現(xiàn)象。光波是電磁波，因此，光波的傳播方向就是電磁波的傳播方向。光波中的電振動(dòng)矢量E和磁振動(dòng)矢量H都與傳播速度v垂直，因此光波是橫波，它具有偏振性。 具有偏振性的光則稱為偏振光。偏振光是指光矢量的振動(dòng)方向不變，或具有某種規(guī)則地變化的光波。按照其性質(zhì),偏振光又可分為平面偏振光（線偏振光）、圓偏振光和橢圓偏振光、部分偏振光幾種。

完全偏振光可分為

（a）線偏振光指光矢量端點(diǎn)的軌跡為直線，即光矢量只沿著一個(gè)確定的方向振動(dòng)，其大小隨相位變化、方向不變，稱為線偏振光。

（b）橢圓偏振光指光矢量端點(diǎn)的軌跡為一橢圓，即光矢量不斷旋轉(zhuǎn)，其大小、方向隨時(shí)間有規(guī)律的變化。

（c）圓偏振光指光矢量端點(diǎn)的軌跡為一圓，即光矢量不斷旋轉(zhuǎn)，其大小不變，但方向隨時(shí)間有規(guī)律地變化。

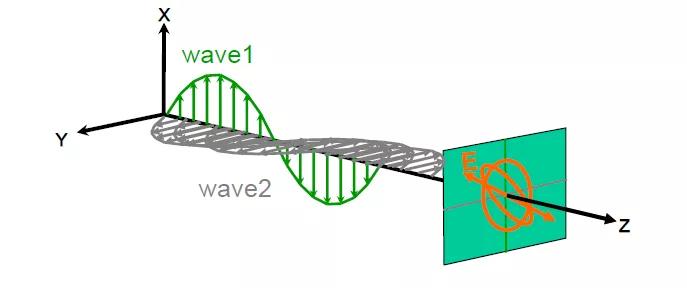
8.部分偏振光

在垂直于光傳播方向的平面上，含有各種振動(dòng)方向的光矢量，但光振動(dòng)在某一方向更顯著，不難看出，部分偏振光是自然光和完全偏振光的疊加。

單個(gè)光子的電場(chǎng)方向沿著單一平面。如前面所述，當(dāng)電場(chǎng)對(duì)齊時(shí)，在相同方向傳播的多個(gè)電場(chǎng)疊加可能導(dǎo)致干擾。然而，正交電場(chǎng)一起傳播沒有干擾。疊加后的電場(chǎng)在通過靜止觀測(cè)器時(shí)的形狀被稱為極化。

9.線偏振光

在圖中，我們表示了沿相同路徑傳播的，具有相同頻率和相同幅度的兩個(gè)光束的電場(chǎng)強(qiáng)度（為了清晰起見，對(duì)它們進(jìn)行了偏移）。一個(gè)在垂直方向上偏振，一個(gè)在水平方向上偏振。當(dāng)沿著傳播方向觀察時(shí)，電場(chǎng)將沿著一條線出現(xiàn)，所以每個(gè)單獨(dú)的波可以看做是線性偏振的。在這種情況下，需要特別注意的是，垂直波的最大值，最小值以及零點(diǎn)與水平波的最大值，最小值以及零點(diǎn)一致，即波是同相的。因?yàn)閮蓚€(gè)波是正交的，所以它們不會(huì)干擾。兩個(gè)波的分量的矢量和疊加在空間中的每個(gè)點(diǎn)處，這導(dǎo)致線性波在垂直方向上偏振45°，如圖2.8所示。如果兩個(gè)波保持同相，但振幅不相等，則結(jié)果將是不同于45°的線性偏振波。確切地說，當(dāng)具有相同頻率的兩個(gè)線性偏振波同相合并時(shí)，所得到的波是線偏振的。

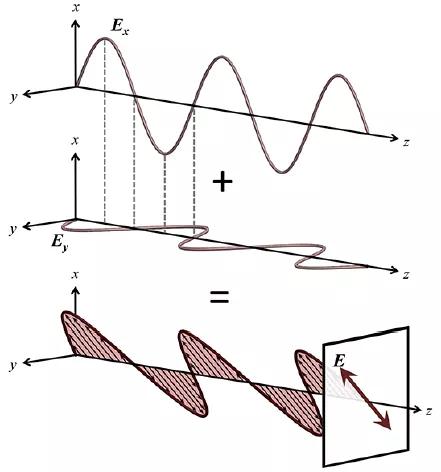
?相同頻率的兩個(gè)正交光波在相同的方向傳播（為了清晰起見，偏移示出）。

由于兩個(gè)波幅度相等，相位相同，因此所得電場(chǎng)為在x-和y-的45°方向的線性偏振。

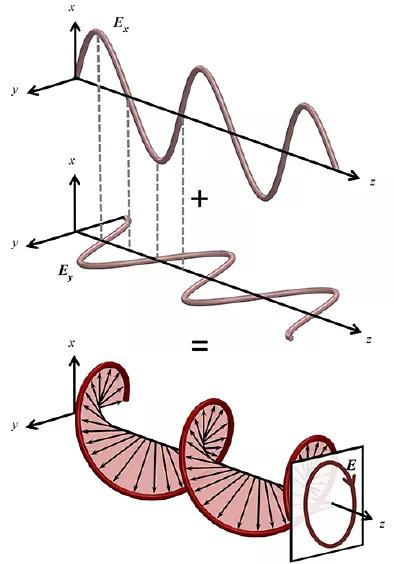
?10.圓偏振光

續(xù)上，將頻率相同，相位為四分之一波長(zhǎng)，振幅相等的兩條線偏振光速組合在一起，產(chǎn)生圓偏振光。我們?cè)俅伪硎玖搜叵嗤窂絺鞑サ南嗤l率和幅度的兩個(gè)光束。同樣，一個(gè)是垂直偏振，一個(gè)是水平偏振。在這種情況下，水平波的電場(chǎng)強(qiáng)度的最大值，零點(diǎn)以及最小值已經(jīng)與垂直波發(fā)生偏離：兩個(gè)波相差四分之一或者90°。當(dāng)兩個(gè)波組合時(shí)，合成波的箭頭的末端不像前面的圖示那樣在平面上來回移動(dòng)。相反，合成波的箭頭末端看，電場(chǎng)以一個(gè)圓的方式移動(dòng)，這稱為圓偏振光，并且僅當(dāng)具有相同頻率的兩個(gè)線性偏振波具有相同的幅度和90°的相位差時(shí)才會(huì)發(fā)生。

11.橢圓偏振光

續(xù)上，如果相移不是90°，或者幅度不相等，那么看到的電場(chǎng)就是在橢圓上移動(dòng)，這稱為橢圓偏振光。具體地說，當(dāng)具有相同頻率的兩個(gè)線偏振波相位不同時(shí)，所得到的波為橢圓偏振。

橢偏儀使用橢圓偏振光，這也是橢偏儀名稱由來的原因。當(dāng)線性偏振光在一定條件下從表面反射時(shí)產(chǎn)生橢圓偏振光。偏振的變化取決于表面（光學(xué)常數(shù)，膜的存在等），橢偏儀通過測(cè)量這種偏振變化來確定被測(cè)樣品的特性。

12.菲涅耳公式

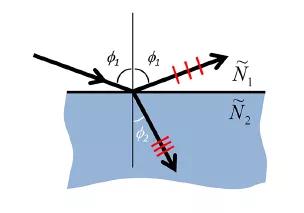
邊界條件描述了通過界面反射和透射的電磁波。這些條件由麥克斯韋方程組推導(dǎo)得到，認(rèn)為切向電場(chǎng)和法向電場(chǎng)在界面上是連續(xù)的。對(duì)于這些條件的解釋得出了光在通過分界面時(shí)振幅和相位的變化。反射或透射發(fā)生在同一界面上，反射光以及透射光的電場(chǎng)分量與入射光的電場(chǎng)分量的比值稱為“菲涅耳系數(shù)”。邊界條件導(dǎo)致了s波和p波的不同方程，因?yàn)樗鼈兊膱?chǎng)分量是沿著不同的平面方向。

在第一介質(zhì)和第二介質(zhì)之間存在一個(gè)單獨(dú)的界面，其中每種介質(zhì)分別由各自的復(fù)折射率來表述。當(dāng)光束從第一介質(zhì)進(jìn)入第二介質(zhì)時(shí)，p波和s波的菲涅爾反射系數(shù)由下列公式得到，

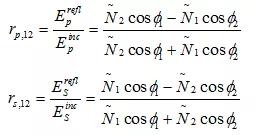
設(shè)入射角和折射角 (與斯涅爾定律相關(guān))。相應(yīng)的菲涅爾透射系數(shù)為，

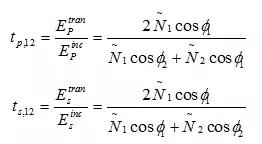
?由于光強(qiáng)與電場(chǎng)強(qiáng)度的平方有關(guān)，因此可以確定反射光以及透射光的光強(qiáng)與入射光光強(qiáng)的比值為：

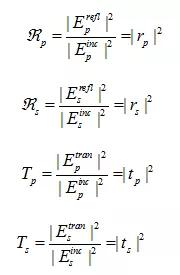
以上稱為偏振反射率和偏振折射率。

13.布魯斯特角

自然光在電介質(zhì)界面上反射和折射時(shí)，一般情況下反射光和折射光都是部分偏振光，只有當(dāng)入射角為某特定角時(shí)反射光才是線偏振光，其振動(dòng)方向與入射面垂直，此特定角稱為布魯斯特角或起偏角。

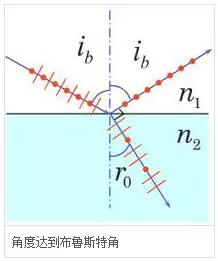
布儒斯特角是折射率的函數(shù)，如上文所述，折射率是波長(zhǎng)的函數(shù)。因此，布儒斯特角是波長(zhǎng)的函數(shù)。“布儒斯特波長(zhǎng)”這個(gè)術(shù)語(yǔ)有時(shí)也被用于單個(gè)入射角度。這僅僅意味著折射率與布儒斯特條件相匹配時(shí)入射光的波長(zhǎng)。

“布儒斯特角”或“偏振角”的概念經(jīng)常被攝影師用來拍攝水下的物體。來自水下物體的光（例如：魚或短吻鱷）通常比水面上反射的光少得多，并且反射光會(huì)使水下的物體變得模糊不清。如果反射光的入射角與布儒斯特角大致相等，就可以根據(jù)正確的方位角調(diào)整偏振器，去除純s偏振的表面反射光，使攝像機(jī)能夠捕捉水下物體所發(fā)出的光。

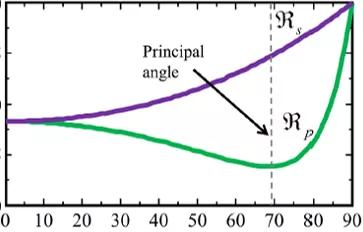
?當(dāng)反射面不透明時(shí)，意味著k不為零，情況會(huì)變得更加復(fù)雜。菲涅耳反射系數(shù)此時(shí)為復(fù)數(shù)，“大于零”和“小于零”的概念并無意義。通常，復(fù)數(shù)的實(shí)部和虛部不會(huì)都為零；

14.復(fù)折射率

當(dāng)光與不同的材料相互作用時(shí)，會(huì)發(fā)生幾種現(xiàn)象。每種都可以通過考慮材料的光學(xué)性質(zhì)來描述。首先，波可以改變方向。圖2.6表示的是到達(dá)空氣和另一種材料之間界面的平面波光束。一些光被反射回到第一介質(zhì)（空氣）中，并且不進(jìn)入第二介質(zhì)。進(jìn)入第二介質(zhì)的光沿新的方向傳播，這部分的光稱為折射光。

第二，光波可以改變相速度。如圖2.6中的三個(gè)平行線表示相應(yīng)的波長(zhǎng)。第一個(gè)介質(zhì)中的相速度比第二個(gè)更快（因此波長(zhǎng)更長(zhǎng)）。第三，光波可以改變振幅。通過光波的分割（一部分反射，剩余部分透射）或者通過穿過吸波材料時(shí)的能量損失可以改變振幅。利用材料的復(fù)合折射率可以描述這些現(xiàn)象。

? 光速與空氣、復(fù)合折射率為?2.的材料的界面之間的相互作用

復(fù)合折射率?由實(shí)部和虛部組成

式中，n是“折射率”或簡(jiǎn)稱“指數(shù)”，k是“消光系數(shù)”，i是虛數(shù)。使用加號(hào)還是減號(hào)取決于其數(shù)學(xué)表達(dá)方式。

15.折射率

光從一種介質(zhì)斜射入另一種介質(zhì)時(shí)，傳播方向發(fā)生改變而使線在不同的交界處偏折的現(xiàn)象即光的折射。折射率指光在真空中的傳播速度與光在該介質(zhì)中的傳播速度之比。材料的折射率越高，使入射光發(fā)生折射的能力越強(qiáng)。 折射率與介質(zhì)的電磁性質(zhì)密切相關(guān)。根據(jù)經(jīng)典電磁理論，εr和μr分別為介質(zhì)的相對(duì)電容率和相對(duì)磁導(dǎo)率。折射率還與頻率有關(guān)，稱色散現(xiàn)象。

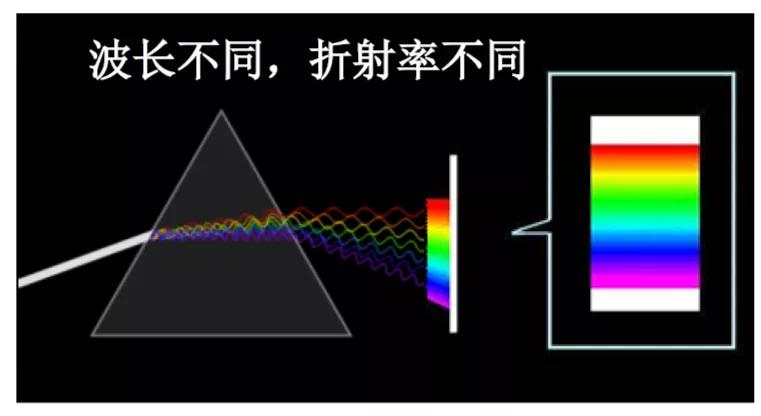
諸如玻璃之類的介電材料的折射率是光在材料中的相速度和在真空中的光速（c）之比的倒數(shù)，即

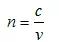
?在氮化硅中，n≈2，光的相速度是光在真空中的一半。

16.消光系數(shù)

消光系數(shù)k 描述介質(zhì)對(duì)光的吸收特性，表示當(dāng)光通過材料時(shí)強(qiáng)度降低的程度。為了方便理解消光系數(shù)，可以先參照吸收系數(shù)定義。

17.吸收系數(shù)

光在介質(zhì)中傳播時(shí)，光的強(qiáng)度隨傳播距離(穿透深度)而衰減的現(xiàn)象稱為光的吸收，光的吸收遵循吸收定律（比爾-朗伯定律）。吸收系數(shù)是比爾-朗伯定律（Beer–Lambert law）中的一個(gè)常數(shù)，符號(hào)位α，被稱為介質(zhì)對(duì)該單色光的吸收系數(shù)。光束沿著Z軸方向入射到吸波材料，在空氣與材料的界面反射時(shí)會(huì)產(chǎn)生一些強(qiáng)度損失。我們用I0表示在材料內(nèi)部時(shí)的強(qiáng)度，在吸波材料中強(qiáng)度的降低由下式給出：

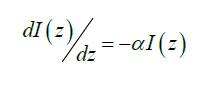
方程的解為：

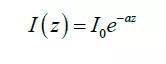
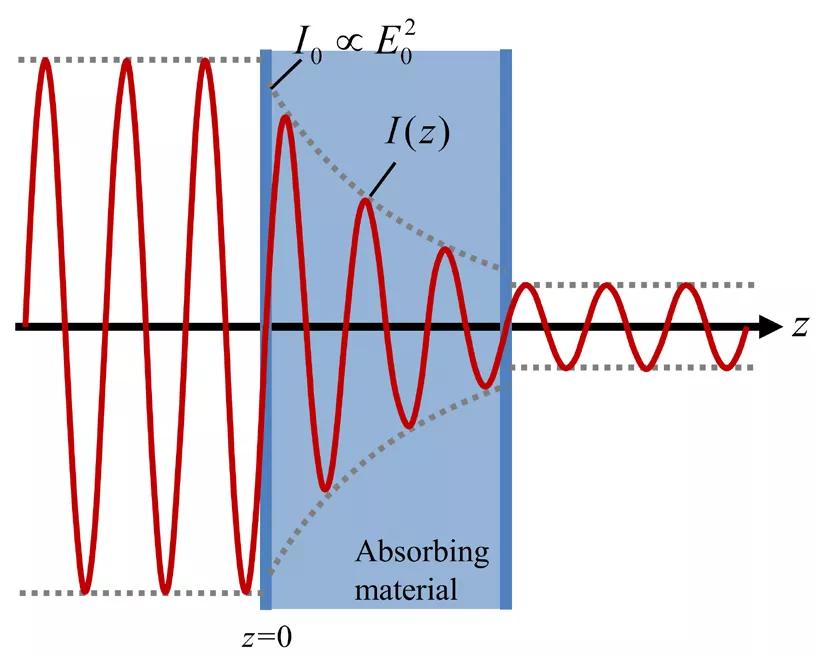
z=0處進(jìn)入吸波材料。不考慮由于每個(gè)界面處的反射造成的損失，強(qiáng)度隨距離材料距離的增大而呈指數(shù)形式減少。可得到消光系數(shù)的定義式：

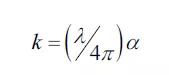
雖然折射率n和消光系數(shù)k通常被稱為材料的“光學(xué)常數(shù)”，但是它們都不是恒定的。它們是光波頻率的函數(shù)（即它們依賴于波長(zhǎng)）。

18.反射率

反射率指的是輸出光與輸入光的強(qiáng)度之比。全反射系數(shù) Rp 和 Rs 指的是輸出光與輸入光的振幅之比。因此，反射率是全反射系數(shù)的大小的平方，即

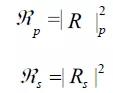
19.透射率

透射是入射光經(jīng)過折射穿過物體后的出射現(xiàn)象。被透射的物體為透明體或半透明體，如玻璃，濾色片等。若透明體是無色的，除少數(shù)光被反射外，大多數(shù)光均透過物體。為了表示透明體透過光的程度，通常用透過后的光通量與入射光通量 之比τ來表征物體的透光性質(zhì)。

τ稱為光透射率對(duì)于透射強(qiáng)度（透射率）可以運(yùn)用類似的公式。反射率和透射率是可由分光計(jì)等裝置測(cè)得的很常見的測(cè)量量。測(cè)量通常處于正入射（0°），因此不需要考慮偏振態(tài)。即使以斜角入射進(jìn)行測(cè)量，也通常使用非偏振光，因?yàn)檫@簡(jiǎn)化了所需的儀器。非偏振反射率或透射率的測(cè)量值將等于 p 和 s 偏振光的平均值。

20.復(fù)介電常數(shù)

材料的光學(xué)性質(zhì)也可以通過復(fù)介電函數(shù)來描述。n和k描述的是光波如何受到材料的影響，復(fù)介電函數(shù)描述的是材料如何受到光波的影響。四個(gè)稱為“本構(gòu)”或“材料”的方程描述的是材料對(duì)電磁輻射的影響。對(duì)于非導(dǎo)電、非磁性材料，電位移D與電場(chǎng)E有如下關(guān)系：

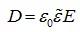
式中，ε0是真空中的介電常數(shù)，e是材料的介電常數(shù)。介電常數(shù)隨光波頻率或波長(zhǎng)變化而變化，所以通常被稱為介電函數(shù)，其可能很復(fù)雜。實(shí)部ε1表示電極化率，描述的是電場(chǎng)如何使材料內(nèi)的電荷分布發(fā)生變形；虛部ε2描述的是材料的吸收特性。復(fù)介電函數(shù)為

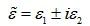
?復(fù)介電函數(shù)與復(fù)折射率之間的關(guān)系為

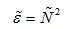
21.?Δ和Ψ

圖中表示了從表面反射的p波和s波。在每一次的反射中，p波和s波都存在一定的相移，并且二者的相移不一定相同。將反射前的p波和s波之間的相位差表示為，反射后的相位差表示。在這里定義一個(gè)參數(shù)Δ，讀作“delta”，

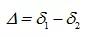
Δ是由反射引起的相移，該值可以在-180°到+ 180°之間（或者0°至360°之間）。

除了相移，反射也會(huì)引起p波和s波振幅的減小，并且對(duì)于二者也不一定是相同的。前文中將p波(Rp)和s波(Rs)的全反射系數(shù)定義為輸出光波與輸入光波的振幅之比，一般來說，這是一個(gè)復(fù)數(shù)。在這里定義參數(shù)Ψ，稱為“psi”，使得

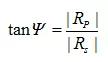
Ψ是其正切值為全反射系數(shù)大小的比值的角度，其值可以在0°至90°的范圍內(nèi)。Ψ和Δ的影響使得線性偏振光在從樣品表面反射后變?yōu)闄E圓偏振光，如圖2.16所示。

22.橢偏基本公式

橢偏測(cè)量采用由p、s分量定向的線性偏振光作為入射光。與樣品的相互作用導(dǎo)致反射光中p光和s光有不同的振幅和相位，產(chǎn)生橢圓偏振光。

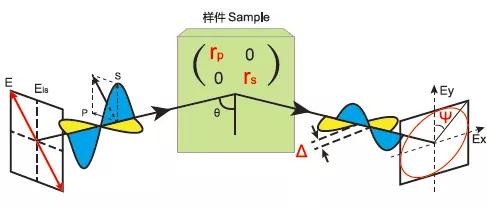
如上所述，定義為全反射系數(shù)大小的比值，因此為實(shí)數(shù)。在這里將復(fù)數(shù)ρ(rho)定義為全反射系數(shù)的復(fù)數(shù)比，如下所示，

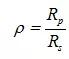
橢偏測(cè)量的基礎(chǔ)公式為：?

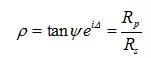
那么tanΨ是ρ的模，指數(shù)函數(shù)是ρ的相位。參數(shù)Ψ和Δ（有時(shí)只有cosΔ）可由橢偏儀測(cè)得。這些參數(shù)表示的是探測(cè)光束的性質(zhì)。關(guān)于樣本的信息包含在全反射系數(shù)中，即在ρ中。應(yīng)當(dāng)注意的是，只要儀器正常工作，那么測(cè)量值Δ和Ψ總是正確的。通過回歸分析可以推導(dǎo)出，例如厚度以及光學(xué)常數(shù)等參量。這些參量的值是否正確取決于我們的假設(shè)模型。例如，如果我們假設(shè)材料是一層基質(zhì)，實(shí)際上是某種材料的薄膜覆蓋在另一種材料的基質(zhì)上，就會(huì)推導(dǎo)出不正確的n和k。這說明橢偏儀測(cè)量出的量是Δ和Ψ。例如厚度和光學(xué)常數(shù)之類的參量是建立在假設(shè)模型的基礎(chǔ)上進(jìn)行計(jì)算得到的。

23.N/C/S

有許多方法可以用來表示由橢偏儀測(cè)量出的偏振態(tài)的變化。Ψ和Δ由于在消光橢偏儀中的早期應(yīng)用而變得十分普遍。在這些早期的單波長(zhǎng)儀器中，光學(xué)元件的應(yīng)用有所限制，除非可檢測(cè)光消失（為零）。在1990年之前，Ψ和Δ的值與主要使用的這些早期器件的光學(xué)讀數(shù)直接相關(guān)。在第3章中，我們將討論現(xiàn)代橢偏儀的操作，并不直接測(cè)量Ψ和Δ。而是收集可能與偏振態(tài)的變化相關(guān)的調(diào)制強(qiáng)度。與儀器測(cè)量的強(qiáng)度最直接相關(guān)的實(shí)際值稱為N，C和S，其與Ψ和Δ的關(guān)系如下：

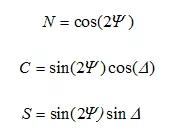
?根據(jù)它們的性質(zhì)，這三個(gè)參數(shù)都在-1和+1之間。對(duì)這三個(gè)參數(shù)的測(cè)定等價(jià)于測(cè)量Ψ和Δ值。在下一章中將會(huì)提到，早期的旋轉(zhuǎn)分析式橢偏儀的配置僅限于測(cè)量N和C，并且將Δ的范圍減小到180°，而不是完全的360°。

24.瓊斯矩陣

橢偏測(cè)量可通過一組線性方程來表示，用以描述p波和s波與樣本之間的相互作用。瓊斯矢量標(biāo)記法將偏振光視為兩個(gè)描述p和s電場(chǎng)的復(fù)數(shù)（幅度和相位）。2×2的瓊斯矩陣可用來表示樣本或可能改變偏振態(tài)的任何光學(xué)元件。對(duì)于各向同性樣品，p波和s波之間不存在交叉極化。換句話說，p偏振光將保持p偏振，并且s偏振光將保持s偏振。然而，它們將會(huì)經(jīng)歷各自的振幅減小和相位變化。這由樣品的Jones矩陣（不同形式）表示，如：

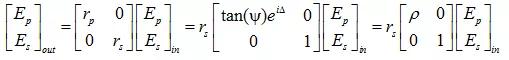
25.穆勒矩陣

瓊斯矢量?jī)H限于表示偏振光，不能表示部分偏振光或非偏振光。對(duì)于這些重要的情況，樣品（或光學(xué)元件）可以使用斯托克斯–穆勒矩陣來表示。這種情況中，每個(gè)光束由構(gòu)成斯托克斯矢量的四個(gè)實(shí)際強(qiáng)度描述，而4×4穆勒矩陣表示光的變換。對(duì)于斯托克斯-穆勒矩陣，各向同性樣本非對(duì)角線2×2塊為零（由于p和s波之間不存在交叉極化），如：

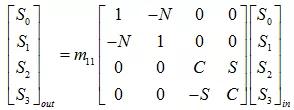
? 其中N，C和S是前文中討論的橢偏參數(shù)，m11是非偏振光的反射強(qiáng)度。在考慮各向同性樣品的穆勒矩陣時(shí)要注意N，C和S的重要性。

26.色散方程

列表的主要缺點(diǎn)是它們不提供有用和高效改變光學(xué)特性的方法。可以調(diào)整每個(gè)單獨(dú)的值，但是這會(huì)引入最大數(shù)量的“空閑”參數(shù)來描述光學(xué)特性。該方法被稱為“逐點(diǎn)”或“逐波長(zhǎng)”擬合。由于相鄰波長(zhǎng)不相互支持，這是非常低效的。相反，允許每個(gè)波長(zhǎng)在不了解相鄰波長(zhǎng)的光學(xué)常數(shù)的情況下變化。這通常導(dǎo)致嘈雜，產(chǎn)生的結(jié)果可能不是唯一的，而且往往是錯(cuò)誤的。

更好更有效的方法是使用色散方程。色散是指不同波長(zhǎng)的光學(xué)常數(shù)的變化。因此，色散方程與光學(xué)特性的波長(zhǎng)依賴關(guān)系相關(guān)。以這種方式，相鄰的波長(zhǎng)有助于彼此支持以達(dá)到一致的答案來匹配光譜數(shù)據(jù)曲線。

我們?cè)谶@里介紹各種色散方程。一些用于透明材料，另一些描述了透明和吸收光學(xué)特性。一些是經(jīng)驗(yàn)性的，純粹是從光學(xué)常數(shù)形狀的觀察而開發(fā)的，沒有這種潛在形狀的物理意義，另一些根植于對(duì)材料及其光學(xué)性質(zhì)的物理理解。無論如何，每個(gè)都提供了以下好處：（1）顯著減少自由參數(shù)的數(shù)量，（2）保持光滑的連續(xù)曲線來描述光學(xué)特性與波長(zhǎng)的關(guān)系，以及（3）允許輕松改變光學(xué)特性的某些屬性。

在描述一些常見的色散方程之前，我們考慮了透明和吸收材料的基本色散形狀，分別被稱為正常和異常色散。