科技改變生活 · 科技引領未來
科技改變生活 · 科技引領未來
注意：這里只先講正整數(shù)如何轉換成二進制，暫時不考慮負數(shù)。
對于一個正整數(shù)，如何求其二進制呢，一般的做法就是，概括起來就一句話：除2取余，逆向取值。比如：
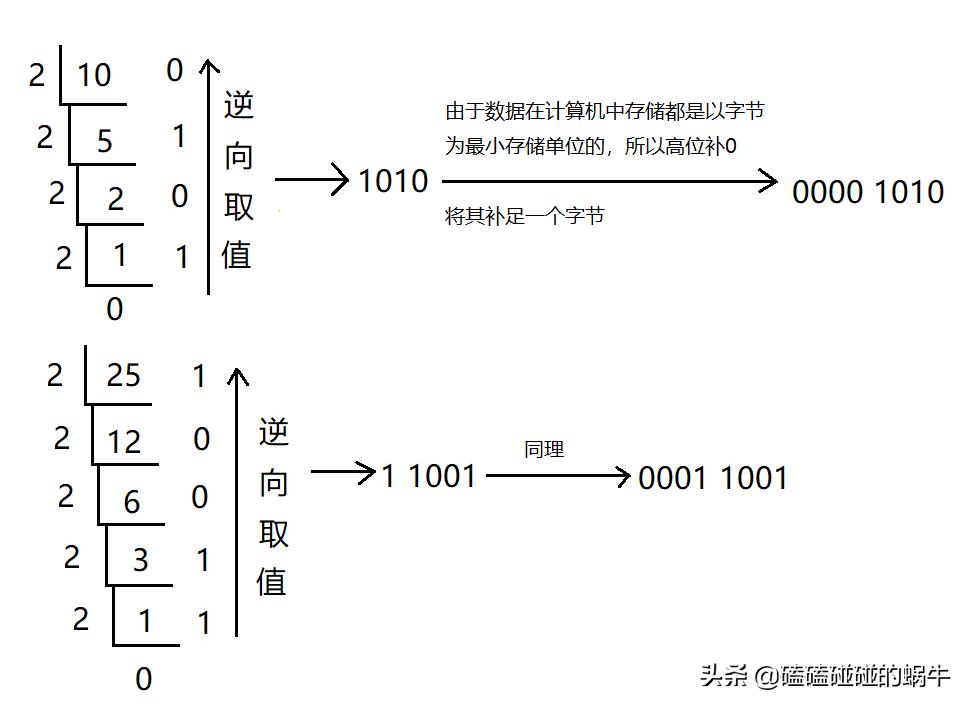
其實，十進制轉換成16進制或8進制或其他位進制，都是同樣的道理，都是除以進制位數(shù)取余，然后再逆向取值。
那么，如何將一個二進制數(shù)轉換成十進制整數(shù)呢？
比如：就拿前面計算出的二進制為例吧
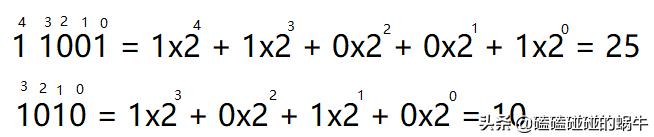
其實，16進制或8進制或其他位進制轉換成十進制，都是采用同樣的方法。
一般公式：
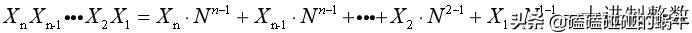
其中，X表示該進制位數(shù)的每一位的數(shù)字；N表示該進制位的進制數(shù)，如若是16進制，則N=16。
補充：二進制數(shù)轉換成十進制整數(shù)的原理
以1010為例，1010轉換成十進制整數(shù)的結果是10。
我們知道，1010是整數(shù)10除2取余、逆向取值得到的。那么，我們也可以反過來，依次將每次除后的結果乘以2再加上余數(shù)，得到上一次除后的結果，如此循環(huán)，就可以逆推過來。具體的過程如下：
首先，我們正向算一下10的二進制：
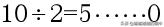
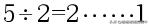
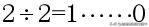
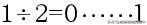
這樣算出來之后，然后逆向取余數(shù)，就得到了10的二進制數(shù)1010。
接著，我們逆著推，算一下1010的十進制數(shù)：
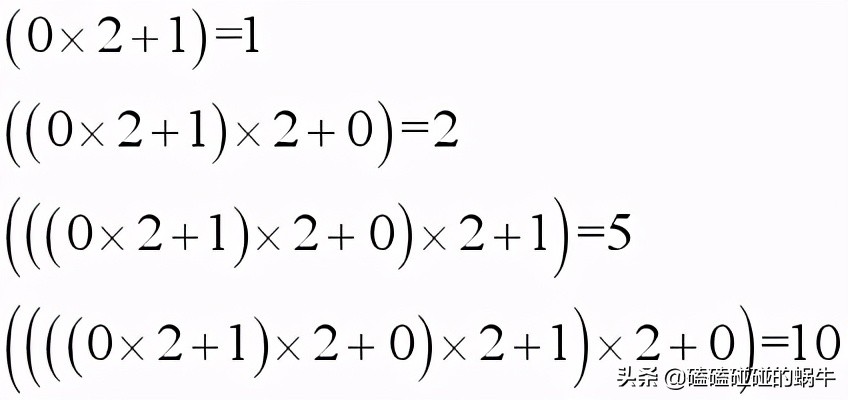
然后將最后一個式子整理一下，把因式都乘進去，就得到了：
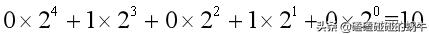
從左往右依次取每一項的系數(shù)，就得到了：01010這個整數(shù)10的二進制數(shù)了。由于二進制數(shù)的最高位取0沒有意義，所以就得到了1010。然后，再把上式改一下，就得到了：
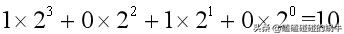
顯然，這與前面“二進制轉換成十進制”的方法一致。
注意：一個整數(shù)被另一個整數(shù)循環(huán)相除(只保留商，不保留余數(shù))，除到最后，所得的商一定會是0。
何悅東