
在2000年之初,克雷數學研究所提出了七個問題,這些問題被認為是至今仍未解決的最困難的問題之一。解決其中任何一個問題都有100萬美元的賞金。
在我寫這篇文章的時候,只有龐加萊猜想得到了解決。格里戈里·佩雷爾曼(Grigori Perelman)在2003年給出了證明,并在2010年被正式授予千禧年獎,但他拒絕了。
我將首先介紹這個猜想(現在是定理),然后根據復雜度的增加順序介紹剩下的未解決的問題。
龐加萊猜想
龐加萊猜想,拓撲學上的一顆明珠,揭開宇宙形狀之謎
任何一個單連通的,閉的三維流形一定同胚于一個三維的球面。
讓我們逐字分析一下。首先,流形是局部具有歐幾里得空間性質的空間,在數學中用于描述幾何形體。這意味著,如果你放大它,它看起來像一條線或一個平面或規則的三維空間等等。一個流形的例子是一個球體,如果你和它相差足夠大并身處其中,它看起來是平的(就像你感覺地球是平的一樣)。流形的維數就是它局部看起來像的空間的維數,例如,一個球局部看起來像一個平面(這意味著它有維數2),一個圓局部看起來像一條線(所以它有維數1),一個思維球體局部看起來像一個三維結構(這一定很神奇,但是我們無法想象)。
如果一個流形是緊湊且無邊界的,那么這個流形就是封閉的(這是一個比較復雜且重要的拓補概念,需要另一篇文章來詳細解釋)。0和1之間的線段有0和1的邊界,所以不是封閉的。圓沒有邊界,所以是封閉的。
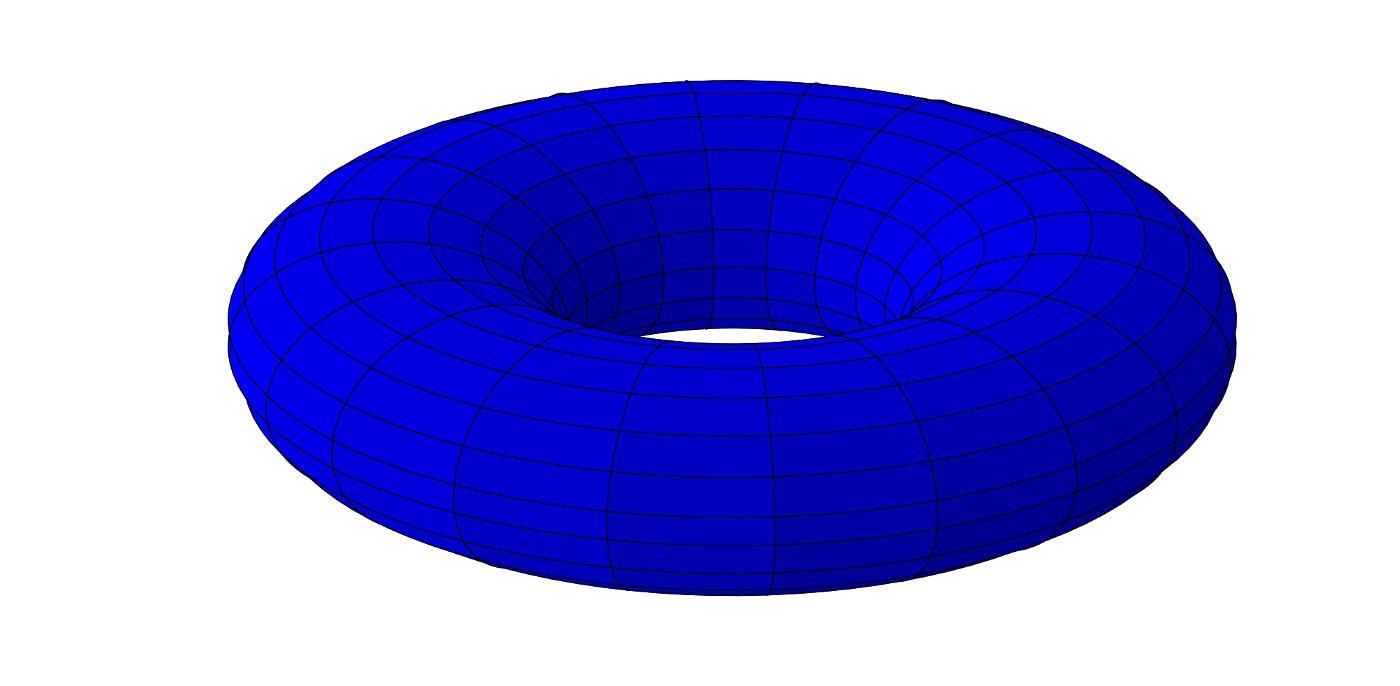
如果一個流形沒有“孔”,則它是單連通的:
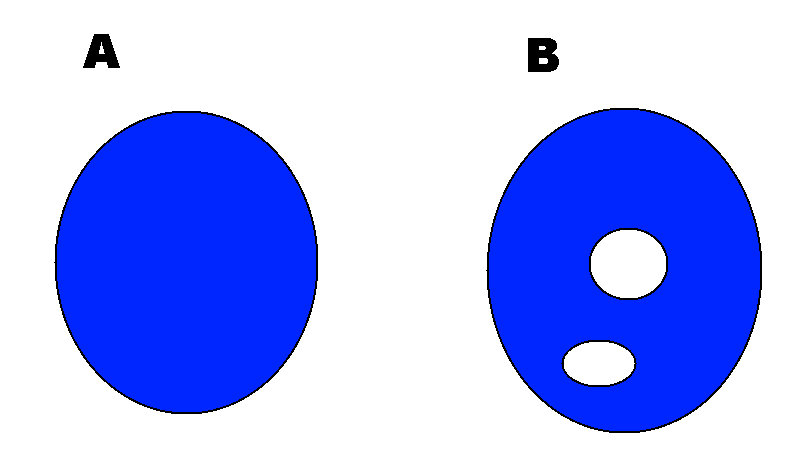
?等效的單連通表述是,每個環可以連續地收縮到一點。
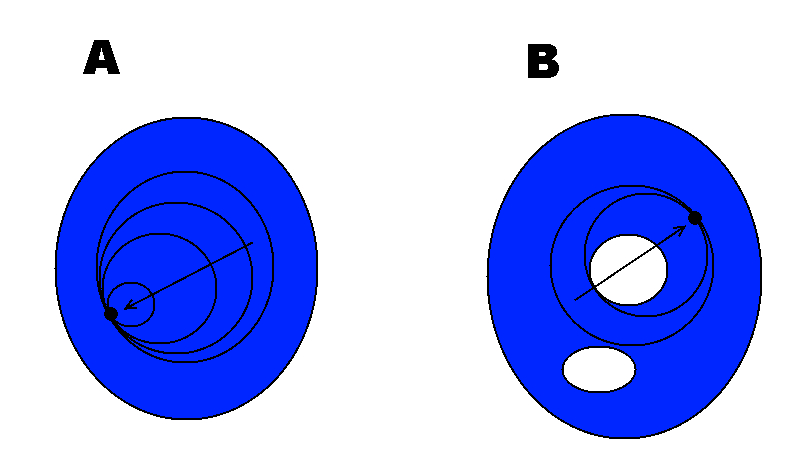
- A中的一個環可以收緊到一個點;B中的一個環被一個孔“卡住”,不能被收緊到一個點。
如果能連續地把一個變形成另一個,然后再變回來,那么這兩個流形是同胚的(允許的變形包括拉伸、擠壓和扭轉,但不允許撕裂和穿孔)。這就引出了著名的甜甜圈和茶杯杯之間的比較(拓補上,它們是同一種東西)。

在拓撲學中,我們想對所有流形進行分類,其中在某個類中的所有流形都是彼此同胚的。在二維空間中,很容易看出,如果流形是封閉的且沒有洞,那么它就相當于一個2維球體(圓面)。很容易確定一個2維流形是否同胚于2維球體。
龐加萊指出,這在三維中也是成立的,即任何封閉的,單連通的3維流形都同胚于3維球面。
2002年,格里戈里·佩雷爾曼通過使用“里奇流”證明了龐加萊猜想。
P vs NP
能否快速驗證每個問題是否可以解決,并快速解決?
問題可以分為不同的復雜性類別。這里我們感興趣的是P和NP類。它們分別表示多項式時間和非確定性多項式時間。
本質上,P問題可以“快速”解決和“快速”驗證。而NP問題(目前)并沒有一個“快速”的解決方案。更具體地說,給定一個輸入大小為n的問題,如果它屬于P類,那么求解它所花費的時間根據某個多項式增加。然而如果它是NP,那么它就會增加得更快。
一個被認為是NP的例子是旅行推銷員問題的(決策問題):
給定一系列城市和每對城市之間的距離,求解訪問每一座城市一次并回到起始城市的最短回路。
解決這個問題很困難,也很費力。如果增加城市的數量,將使求解時間的增加比任何多項式都要快得多。
另一方面,一個P問題的例子是驗證一個數字是否在給定的列表中。這很容易解決,也很容易檢查,如果你將列表的大小翻倍,所花費的時間也會翻倍(所以所花費的時間不會增長得太快)。
P vs NP問題問的是,是否NP問題和P問題是不同的。否則,是否存在一些秘密或隱藏的算法可以快速解決以前認為困難的問題(NP問題)?
納維爾-斯托克斯問題,存在性和平滑性
改變世界的方程之納維爾-斯托克斯方程,堪稱最難的物理學方程
在三維空間和時間中,給定初始速度,是否存在一個光滑且具有全局定義的矢量速度和標量壓力場來求解納維爾-斯托克斯方程(Navier–Stokes equations)?
納維爾-斯托克斯方程是描述三維流體運動的兩個非線性偏微分方程。它是兩個方程的集合,將速度矢量場和它的變化率與壓力場聯系起來,也就是作用于液體的外力。方程式是這樣寫的:
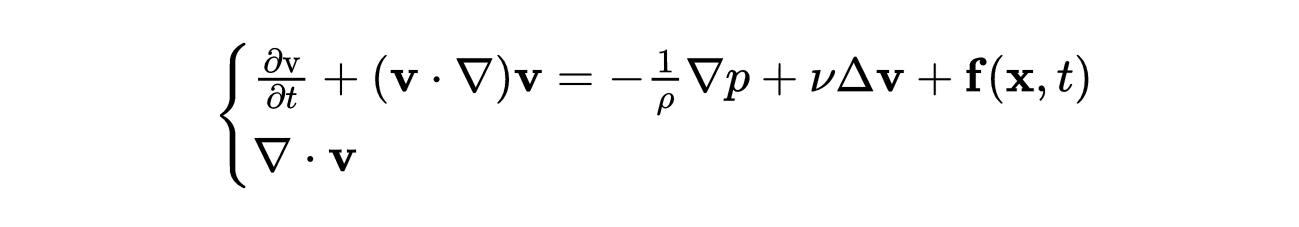
我們不會深入研究每一項的含義,但本質上,第一個方程是牛頓的F=ma。第二個方程也很簡單,是質量守恒方程,要求流體不可壓縮。
一個“有效”的解有兩個條件:
- 向量場v和標量場p是全局定義的,在整個空間上是連續的。
- 總動能是有界的。(v的范數的平方在整個空間上的積分是有界的)。
所以納維爾-斯托克斯問題可以歸結為下面兩種情況中的一種:
- 正面表述:給定f = 0和初始速度場(必須滿足一定條件),存在滿足(1)和(2)的速度場和壓力場。
- 反面表述:存在一個初始矢量場和外力場,其中不存在滿足(1)和(2)的解。

黎曼猜想(假設)
一文搞懂黎曼假設,解析數論的里程碑,質數理論的珠穆朗瑪
黎曼函數的所有非平凡零點的實部都等于1/2嗎?
讓我們分解一下。首先,黎曼ζ函數由下式定義:
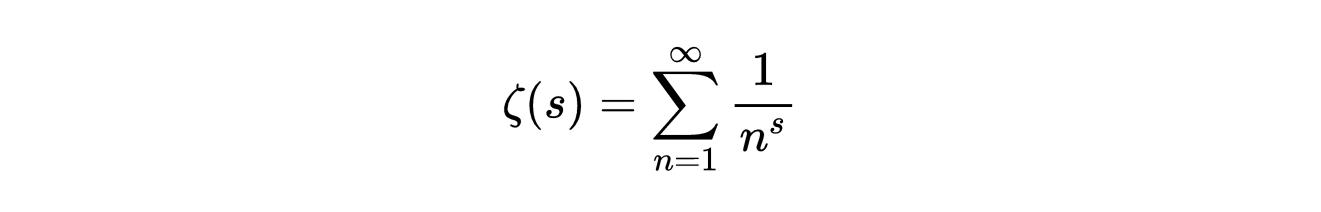
它對 s > 1時有效。注意,當s = 1時,函數簡化為調和級數。我們可以做一些奇特的數學運算,用下面的函數關系將函數解析到復平面上(除了s = 0和1時):
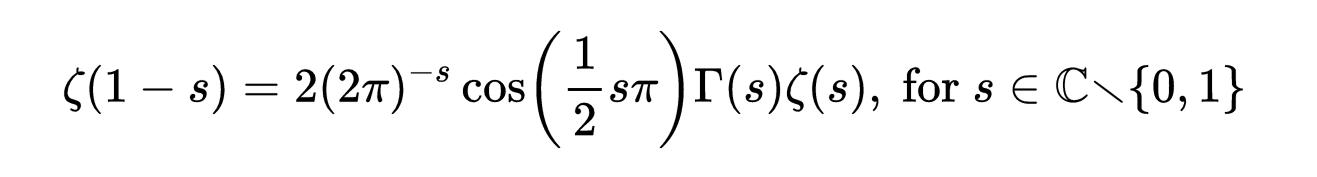
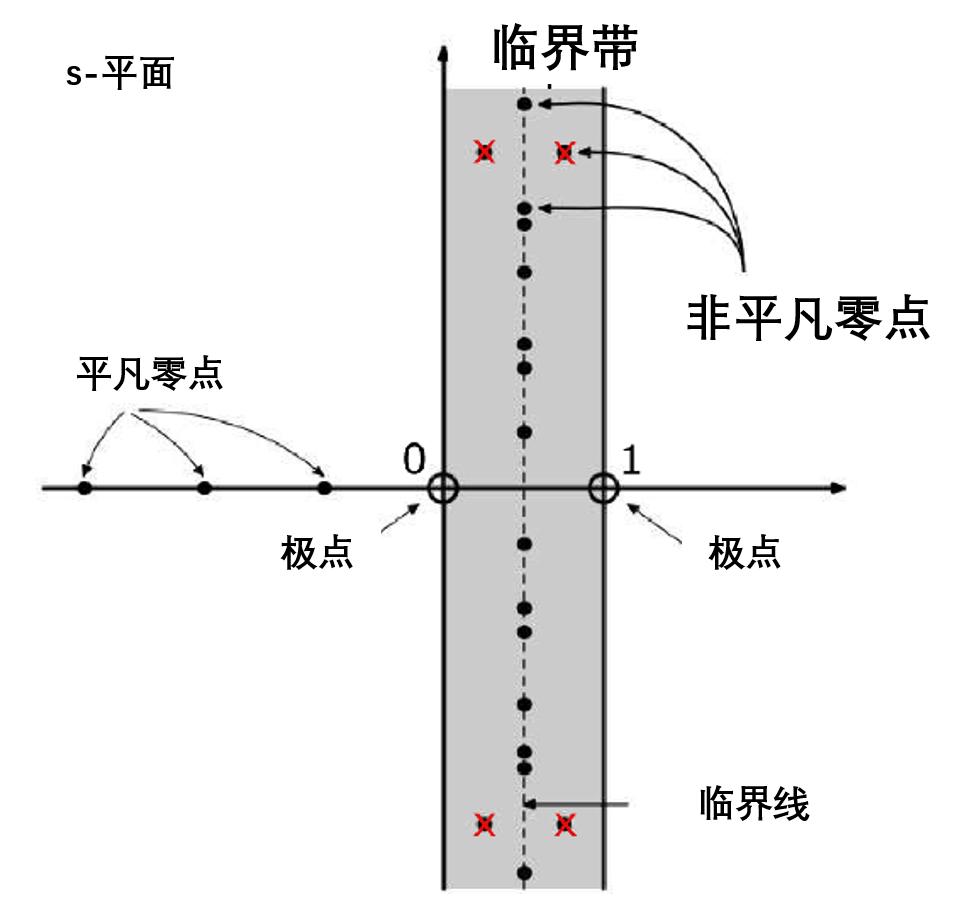
現在我們要求s, ζ(s) = 0。既然奇數負整數的余弦值是0,那么ζ(-2n)對于正整數n是0。這些被稱為平凡零點,因為余弦函數的性質使它為零。相反,我們感興趣的是非平凡零點的情況。
已知所有非平凡零都有0到1之間的實部,稱為臨界帶。結果是,如果s是一個非平凡零點(即ζ(s) = 0且s不是負偶數),那么對于一些值y,s = 1/2 + iy(即s的實部是1/2),這就是所謂的臨界線。
伯奇和斯溫納頓-戴爾猜想
給定一條?上的橢圓曲線E,其代數秩總是與解析秩重合嗎?
橢圓曲線E,為方程y^2=x^3+Ax+B的解集,且判別式?=-16(4A^3+ 27B^B)≠0。這個約束條件保證了曲線足夠好。
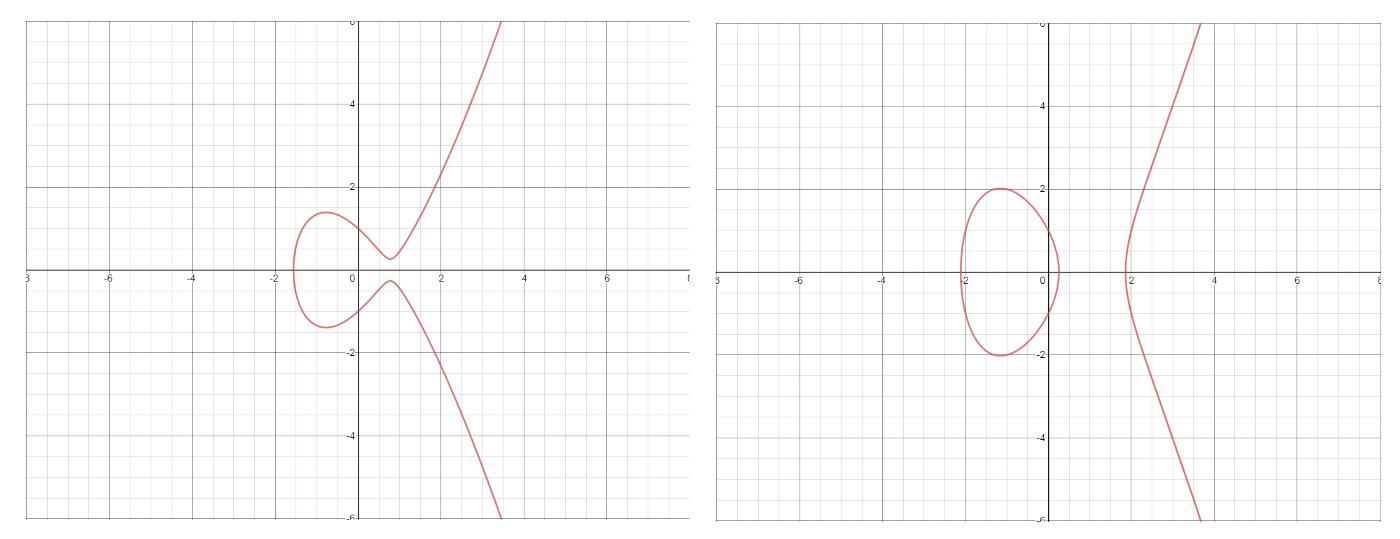
- 兩個橢圓曲線。左邊:y^2=x^3-1.5x+1。右邊:y^2=x^3-4x+1
?現在我們要求x和y是有理的,從而限制了橢圓曲線的解。這就是我們說的?上的曲線。現在我們可以用這條曲線E來組成一群E(?)。我們做了一個很簡潔的二元運算:給定兩個點,我們畫一條直線通過它們,找到與E的第三個交點并將它反射到x軸上。
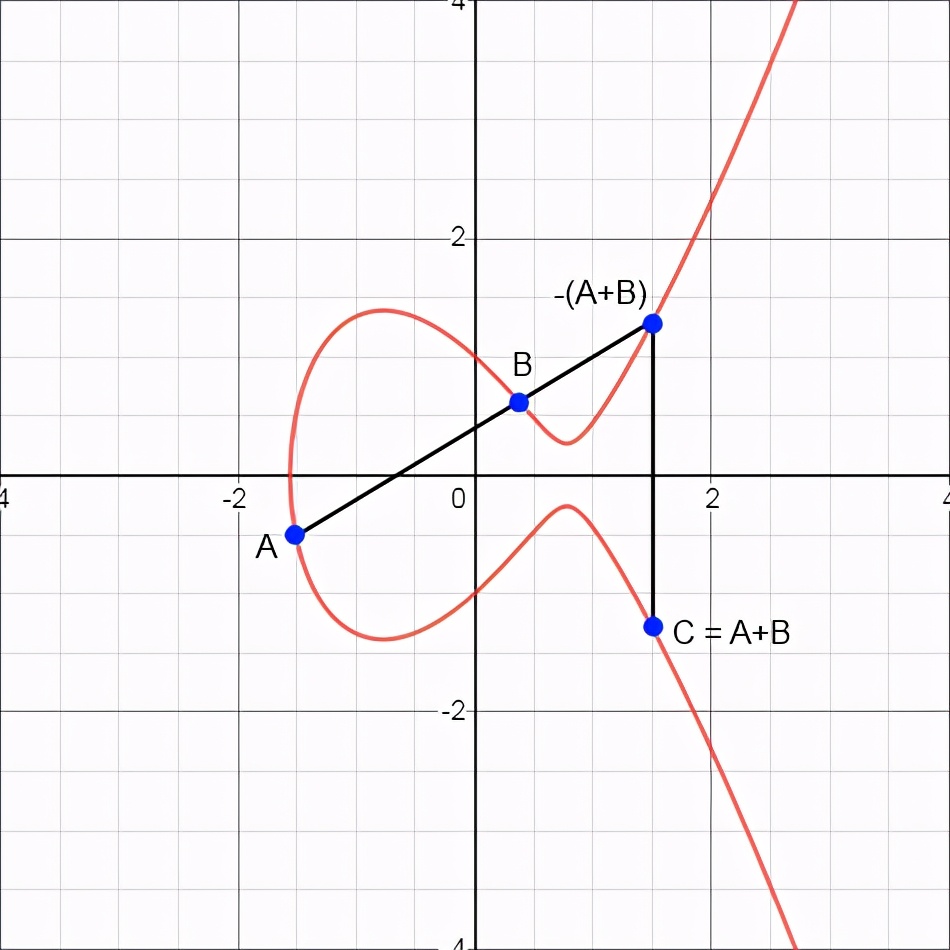
為了使它完全成為一群,我們需要在無窮遠處添加一個點作為群的標識。
第一個自然的問題是,我們可以推斷出E(?)的結構是什么?
莫德爾和威爾(Mordell and Weil)的結果告訴我們,E(?)是有限生成的,可以寫成:
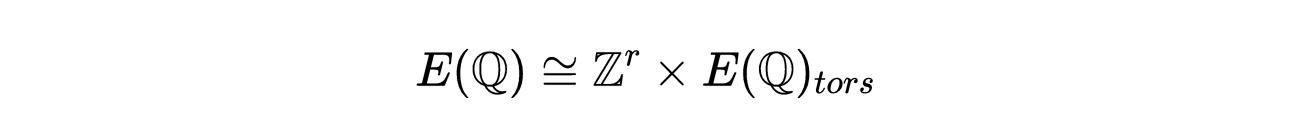
其中E(?)_tors是E(?)中所有有有限順序的點。r被稱為曲線E的代數秩。
現在我們有了前半部分。現在我們需要理解解析秩。
現在讓我們進一步限制解,考慮在有限域p上,其中p是一個素數,我們定義以下值:

最后是E在s處的L級數:
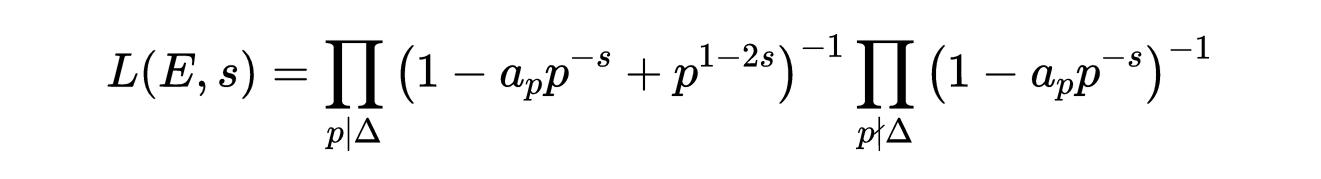
回憶一下,?是橢圓曲線的判別式。那么我們可以將L展開成一個泰勒級數,圍繞s = 1展開:
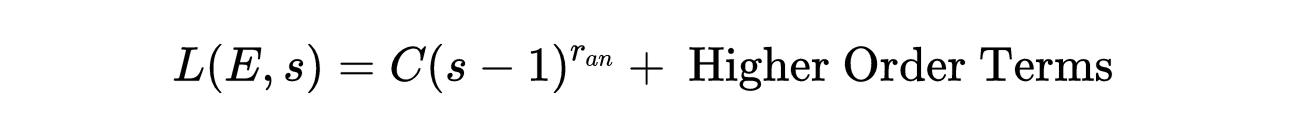
這里,r_an是曲線的解析秩。
終于!我們可以把伯奇和斯溫納頓-戴爾猜想簡單地寫成:

這些都意味著什么呢?結果是,計算代數秩相當困難,而解析秩稍微容易一些。這個猜想在解析領域和代數領域之間架起了一座橋梁。
楊-米爾斯存在性與質量間隙
給定任何緊湊的簡單規范群G,在?? (?^4)上,是否存在一個非平凡量子楊-米爾斯理論,具有質量間隙 Δ > 0?
這里有一個簡短的免責聲明:我不是粒子物理學的專家,所以我將在這里給出我最好的表面理解(有錯誤之處,歡迎指正)。
這個問題要求的是讓現代物理學在數學上變得嚴謹。
我們從規范對稱的概念開始,這些本質上是我們如何描述一個物理系統的自由度。艾美·諾特的一個簡單定理是,對于每一種對稱,都有相應的守恒定律。例如:
- 時不變(也就是說,無論你是現在開始實驗,還是在喝完茶5分鐘后開始實驗)直接產生能量守恒
- 平動不變性引起動量守恒
接下來,我們來看楊-米爾斯理論。
勞倫斯·克勞斯(Lawrence Krauss)給出了最好的解釋。想象一個象棋棋盤,如果你把每個白方塊換成一個黑方塊,每個黑方塊換成一個白方塊,那么游戲基本上是相同的。沒有發生太多的改變,所以這是一個相當簡單的對稱。
但是現在想象一下,我局部地改變了某個方塊的顏色,并且在整個棋盤上隨心所欲地這么做。棋盤看起來會很奇怪,但我可以寫一本規則手冊來解釋我做的所有交換。這個規則手冊規定了游戲如何進行。

所以,讓我們回顧一下:
規范群是一個系統的一組(可能非常奇怪的)對稱,這就產生了守恒定律,我們可以寫一本“規則手冊”,這是一個定義粒子如何相互作用的場,這就是楊-米爾斯理論。
這已經在電磁力和強核力的情況下做過了,它們完全用量子電動力學和量子色動力學來描述。
楊-米爾斯的存在論(我們馬上就會講到質量間隙)所要求的是,這種描述是否適用于所有的四種基本力?更進一步,他們能統一嗎?

說到質量間隙,這些場中的一個激發實際上是粒子。質量間隙本質上是規定這些粒子的質量必須在下面,這樣你就找不到任意輕的粒子。這就是我們在自然界中觀察到的。它被稱為質量間隙,因為在0和最輕的粒子之間有一個間隙。
因此,楊-米爾斯理論要想“擅長”描述現實,就提出這個質量間隙。
霍奇猜想
設X為非奇異復射影流形。那么X上的每個霍奇類可以寫成X復子簇上同調類有理系數的線性組合嗎?
這是一個非常了不起的猜想。這里我就不詳細講了,因為這很難理解(未來幾天,我會專門寫一篇文章來解釋)。
代數方程和幾何圖形之間有一種自然的交換。x^2+y^2-1= 0的解形成一個圓x+y-1=0形成一條直線。

所以我們可以想出一些瘋狂的方程和它的解形成一個(有時非常復雜的)形狀,這些被稱為代數循環。如果這些代數循環足夠光滑,那么它們可以被稱為流形(回想一下龐加萊猜想)。
所以代數循環可以形成流形,如果我們加入更多的方程我們就可以得到流形上的代數循環。

- 把z = 0加到x^2+y^2+z^2=1上,得到一個圓
現在從拓撲學的角度來看,我們可以在流形上畫一些瘋狂的形狀然后把這些形狀組合在一起,如果它們可以互相變形的話。它們被分成同調類。

這看起來就像我們上面所考慮的交換:我們正在從對形狀的代數描述轉向幾何描述。問題是,給定一個流形,什么時候一個同調類包含一個可以被描述為該流形上的一個代數循環的形狀?
不幸的是,我們一直在研究正則歐幾里得空間中的流形。霍奇猜想研究存在于n維空間中的復射影流形。
霍奇想出了一個巧妙而優雅的想法來判斷一個同調類是否等同于一個代數循環,這在本質上就是霍奇猜想。
想了解更多精彩內容,快來關注老胡說科學

